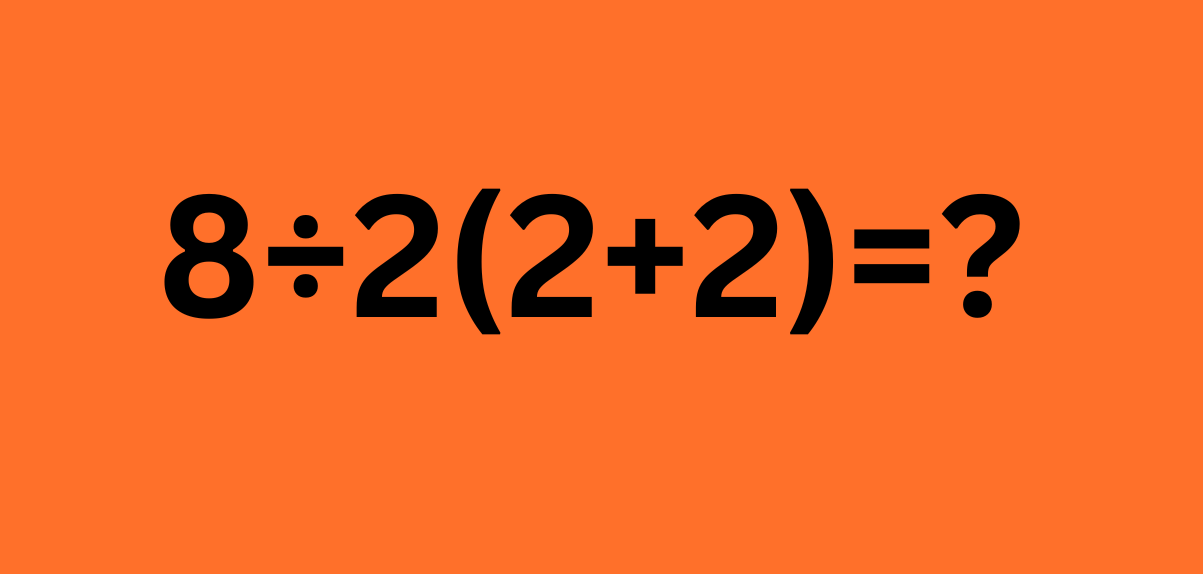Het internet is een broedplaats voor eindeloze uitdagingen, raadsels en virale problemen die de nieuwsgierigheid van miljoenen mensen prikkelen. Van puzzels die mensen op werkplekken afleiden tot uitdagingen die hele families laten discussiëren aan de eettafel, het lijkt erop dat iedereen af en toe verstrikt raakt in een raadsel dat hen doet nadenken. Een van de meest memorabele voorbeelden van zo’n virale uitdaging is een wiskundeprobleem dat in 2019 online verscheen en al snel overal ter wereld aandacht trok. Dit eenvoudige maar o zo complexe probleem leidde tot verhitte discussies, niet alleen tussen gewone internetgebruikers, maar ook onder wiskundigen en wetenschappers. Hoe kan één simpele som zoveel opschudding veroorzaken?
Het raadsel, dat in een enkele tweet werd gedeeld, luidde: 8 ÷ 2(2 + 2). Op het eerste gezicht lijkt het niet meer dan een basiswiskundeprobleem dat velen van ons in de schooltijd waarschijnlijk zonder al te veel moeite zouden oplossen.

Echter, zodra mensen begonnen met het oplossen ervan, kwamen ze tot de ontdekking dat er niet één correct antwoord was, maar twee.

Dit leidde tot een kloof: sommigen beweerden dat het juiste antwoord 16 was, terwijl anderen volhielden dat 1 de correcte uitkomst moest zijn.

Wat volgde was een online vuurstorm van meningen en discussies, waarbij zelfs wiskundigen verdeeld raakten over welke methode nu precies correct was.

Content:
De Verwarring
Het probleem begon op Twitter, toen een gebruiker de som deelde en zijn volgers vroeg om de oplossing te vinden.

Al snel overspoelde een golf van reacties het internet, waarbij mensen uiteenlopende antwoorden gaven en elkaar probeerden te overtuigen van hun gelijk.

Maar hoe kon een ogenschijnlijk simpele vergelijking zoveel discussie losmaken?

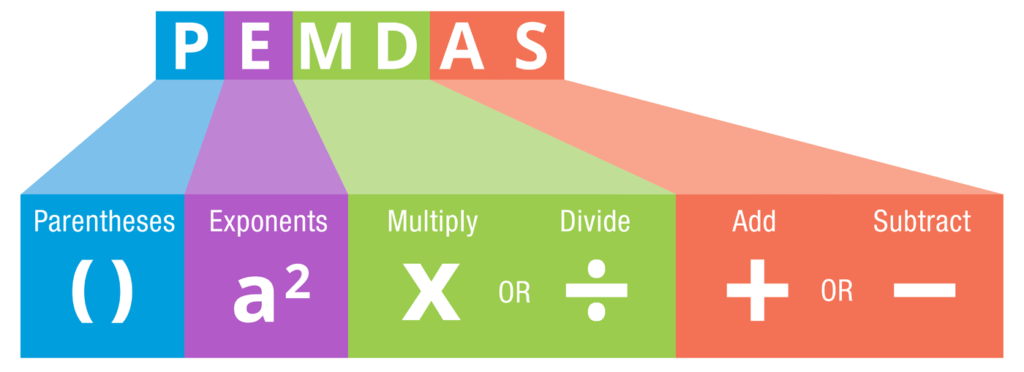
Om het probleem goed te begrijpen, moeten we eerst de basisregel van wiskunde doorlopen die bekend staat als de volgorde van bewerking.

Deze regel, meestal weergegeven met het acroniem PEMDAS, is de sleutel tot het correct oplossen van wiskundige vergelijkingen. PEMDAS staat voor:
- P: Parentheses (Haakjes)
- E: Exponents (Exponenten)
- MD: Multiplication and Division (Vermenigvuldiging en Deling)
- AS: Addition and Subtraction (Optellen en Aftrekken)
Volgens deze regel moeten eerst de bewerkingen binnen de haakjes worden opgelost, gevolgd door exponenten, dan vermenigvuldiging en deling (van links naar rechts), en tenslotte optellen en aftrekken (eveneens van links naar rechts).
Met deze regel in gedachten zou het wiskundeprobleem als volgt moeten worden aangepakt:
- 8 ÷ 2(2 + 2): Los eerst de som in de haakjes op. Dit geeft ons:
8 ÷ 2(4). - Vervolgens moeten we verder met de deling en vermenigvuldiging van links naar rechts. Dus:
8 ÷ 2 = 4, en daarna:
4 × 4 = 16.
Volgens deze stappen zou het juiste antwoord op het probleem 16 moeten zijn. Maar zoals met veel wiskundige problemen, is er een andere manier om het aan te pakken die een compleet ander resultaat oplevert.

Een Alternatieve Interpretatie
De alternatieve manier om het probleem te benaderen volgt een iets andere logica. In plaats van de vergelijking van links naar rechts op te lossen, stelt deze methode dat de uitkomst van de haakjes meteen vermenigvuldigd moet worden met het getal dat ervoor staat. Dit betekent dat de vergelijking wordt opgevat als:
8 ÷ [2(4)].
In dit geval wordt de haakjesnotatie behandeld als één geheel, waardoor het deel tussen haakjes eerst moet worden opgelost. Dit verandert de vergelijking in:
8 ÷ 8, wat resulteert in een quotiënt van 1.
Deze manier van oplossen komt voort uit een verschil in de interpretatie van de volgorde van bewerkingen, waarbij sommigen de vermenigvuldiging die direct naast de haakjes staat, voorrang geven boven de deling.
Hierdoor ontstaan er twee kampen: het ene kamp dat uitkomt op 16 en het andere kamp dat volhoudt dat 1 correct is.
De Rol Van Conventies
De discussie over dit probleem toont aan dat wiskunde, hoewel het een exacte wetenschap lijkt, ook afhankelijk is van conventies en interpretaties.

Mike Breen, vertegenwoordiger van de American Mathematical Society, verklaarde in een interview dat volgens de strikte volgorde van bewerkingen het juiste antwoord 16 zou moeten zijn.

Maar hij voegde eraan toe dat de vergelijking, zoals die is geschreven, dubbelzinnig is en ruimte laat voor verschillende interpretaties.

“In wiskunde zijn er soms dubbelzinnigheden. Wiskundigen proberen de regels zo precies mogelijk te maken, maar het kan voorkomen dat er meerdere interpretaties mogelijk zijn.
In dit geval zou ik iemand die zegt dat het antwoord 1 is, niet direct corrigeren, hoewel volgens de conventionele regels 16 het juiste antwoord is,” legde Breen uit.
Deze dubbelzinnigheid in wiskunde doet denken aan andere vormen van taal of cultuur waarin conventies een grote rol spelen.
Een eenvoudige vergelijking kan net zoals een woord meerdere betekenissen hebben, afhankelijk van de context waarin het wordt gebruikt.
Dit werd ook benadrukt door Rhett Allain, een natuurkundeprofessor aan de Southeastern Louisiana University.
Hij suggereerde dat het probleem duidelijker had moeten worden genoteerd, bijvoorbeeld als 8 ÷ (2 × (2 + 2)), wat zonder twijfel een uitkomst van 1 zou hebben opgeleverd.
“Conventies zijn belangrijk,” aldus Allain. “We hebben bepaalde regels en afspraken over hoe we dingen moeten opschrijven en interpreteren, net zoals we afspraken hebben over spelling.
Maar zelfs in taal kunnen er variaties zijn, zoals het verschil tussen ‘grijs’ en ‘grijs’. We begrijpen nog steeds wat er bedoeld wordt, ondanks die variaties.”
Wat Kunnen We Hieruit Leren?
Het virale wiskundeprobleem laat zien dat zelfs de meest eenvoudige sommen een bron van verwarring en discussie kunnen zijn wanneer ze niet op een volledig eenduidige manier worden gepresenteerd.
Wiskunde is een vak waarin duidelijke regels gelden, maar zelfs binnen die regels kan er ruimte zijn voor verschillende interpretaties.
Dit kan leiden tot frustratie, maar ook tot interessante discussies over de aard van wiskundige conventies en hoe we deze toepassen in ons dagelijks leven.
Wat we hiervan kunnen leren, is dat duidelijkheid in wiskundige notaties essentieel is. Net zoals taal soms meerduidig kan zijn, geldt dat ook voor wiskundige uitdrukkingen.
Daarom is het belangrijk om helder te communiceren en de juiste conventies te volgen om misverstanden te voorkomen.
Key Points:
- Het wiskundeprobleem 8 ÷ 2(2 + 2) veroorzaakte online verdeeldheid, met antwoorden variërend van 16 tot 1.
- Volgens de PEMDAS-regel zou het antwoord 16 moeten zijn, omdat de som in de haakjes eerst moet worden opgelost en vervolgens de deling van links naar rechts wordt uitgevoerd.
- Een alternatieve interpretatie stelde dat de vergelijking moest worden gelezen als 8 ÷ [2(4)], wat resulteert in 1.
- Wiskundigen zoals Mike Breen gaven toe dat de vraag dubbelzinnig is, wat leidde tot verschillende interpretaties, zelfs onder experts.
- Het probleem laat zien hoe belangrijk het is om wiskundige notaties duidelijk en eenduidig te presenteren, om verwarring te voorkomen.
DISCLAIMER: De informatie in dit artikel is uitsluitend bedoeld voor educatieve en informatieve doeleinden en mag niet worden beschouwd als financieel, juridisch of medisch advies. SPECTRUM Magazine en de auteur zijn niet verantwoordelijk voor enige beslissingen of acties die worden ondernomen op basis van de informatie in dit artikel. Raadpleeg altijd een gekwalificeerde professional voordat u belangrijke financiële, juridische of medische beslissingen neemt.