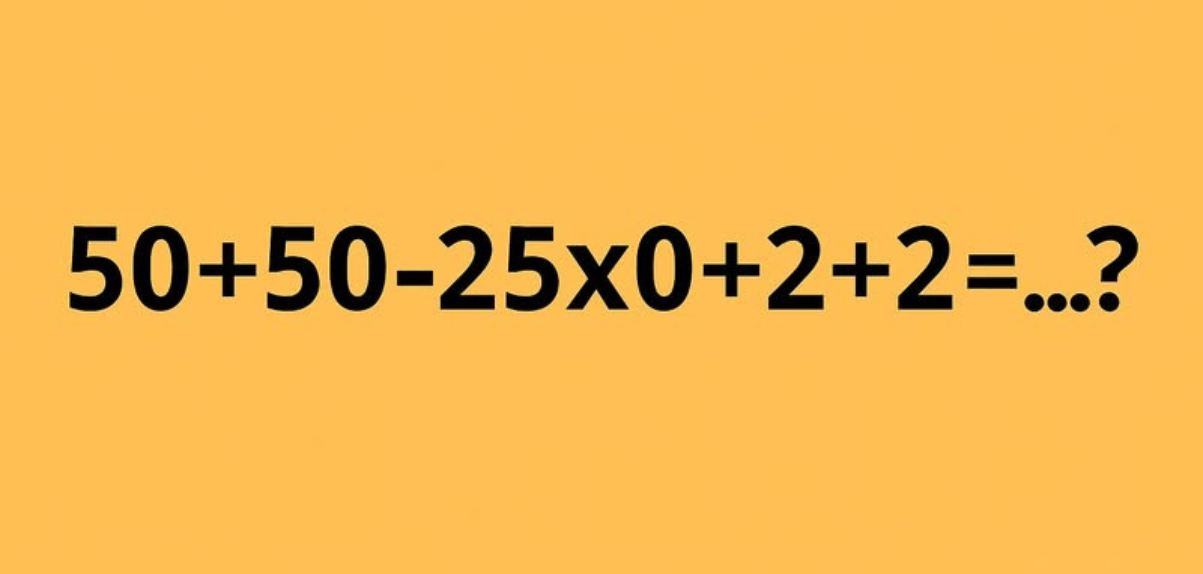Veel mensen denken niet meer aan rekenen, maar een uitdagende som is nog steeds een leuke manier om je brein scherp te houden. Probeer deze simpele opgave eens en bewijs dat je nog steeds snel van geest bent, ook zonder recente wiskundetraining. Laat de puzzel je uitdagen en ervaar hoe fijn het is om stap voor stap tot het juiste antwoord te komen. Leeftijd maakt niet uit, een alert, actief en leergierig brein blijft belangrijk, zelfs na school.
Veel mensen genieten van het oplossen van dit soort puzzels, omdat ze op een ontspannende manier de hersenen stimuleren en tegelijkertijd een duidelijk doel bieden. Door je te concentreren op één probleem kun je je aandacht, geheugen en nauwkeurigheid trainen zonder dat het veel inspanning kost. Onderzoek toont aan dat het regelmatig oplossen van dit soort puzzels bijdraagt aan een beter werkgeheugen, verbeterde concentratie en een sneller denktempo, wat direct merkbaar kan zijn in het dagelijks leven.

Deze rekenvragen zijn luchtig én leerzaam voor jong en oud, waardoor ze uitstekend geschikt zijn om basisprincipes van wiskunde op te frissen op verschillende niveaus. Het samenspel van leren en plezier maakt de ervaring positief en motiverend, verlaagt de drempel om het vaker te doen en helpt om wiskundige regels weer vanzelfsprekend toe te passen wanneer dat nodig is.

Content:
Waarom raadsels goed zijn
Het oplossen van een puzzel gaat verder dan vermaak en traint de hersenen doelgericht. Je vergroot je concentratie, versterkt logisch redeneren en leert flexibeler te denken wanneer een uitkomst tegenvalt. Deskundigen benadrukken dat variatie in denkopgaven belangrijk is om alert te blijven, en dat regelmaat in korte puzzelmomenten het effect verder vergroot.

Meerdere studies tonen aan dat regelmatig puzzelen cognitieve vaardigheden kan aanscherpen en het herkennen van patronen verbetert. Je ontdekt efficiëntere oplossingsroutes, leert foutjes sneller te corrigeren en ontspant ondertussen ook mentaal. Dat geheel werkt positief door op je humeur, je zelfvertrouwen en je algemene welbevinden.
Het oplossen van puzzels verbetert de samenwerking tussen verschillende delen van de hersenen en traint het denkvermogen door tegelijkertijd verschillende processen als geheugen, aandacht en probleemoplossend vermogen aan te spreken. Het gaat hierbij om meer dan slechts een spelletje; het is een gezonde gewoonte die het brein actief, flexibel en alert houdt en mogelijk zelfs helpt bij het vertragen van cognitieve achteruitgang op latere leeftijd.
De uitdaging
Hoewel de rekensom eenvoudig lijkt, kunnen er verschillende antwoorden ontstaan, wat aantoont dat de opgave meer aandacht nodig heeft. Blijf gestructureerd werken, respecteer de volgorde van bewerkingen en controleer iedere stap voor een stevig onderbouwde uitkomst.
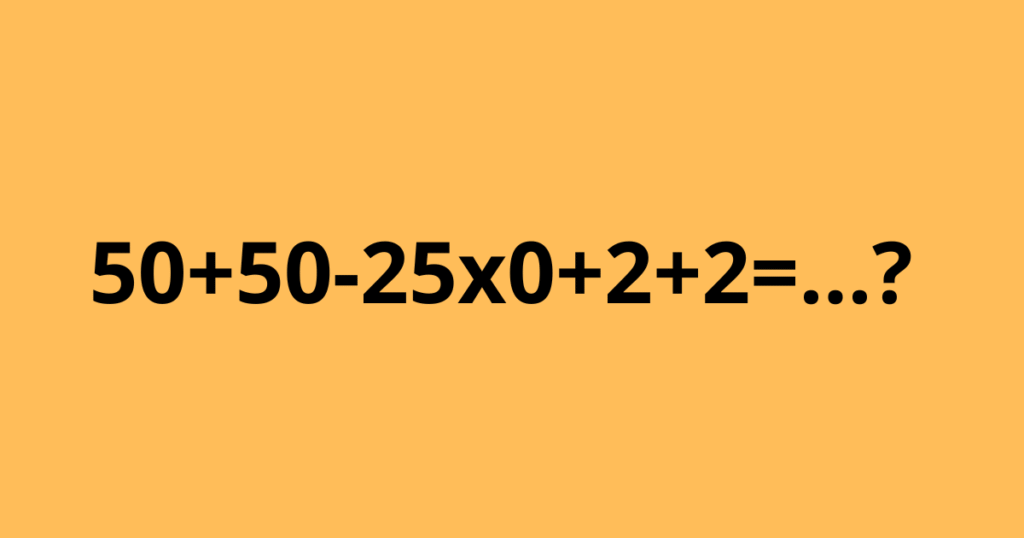
50 + 50 – 25 × 0 + 2 + 2 = ?
Om correct te rekenen volg je altijd de vaste bewerkingsvolgorde die je al vroeg leert. Door stap voor stap te werken voorkom je vergissingen, behoud je overzicht en kun je tussentijdse resultaten controleren.
Deze taak laat zien dat logica en structuur zwaarder wegen dan snelheid. Wie methodisch te werk gaat, ontdekt dat dit uiteindelijk juist sneller én nauwkeuriger werkt. Je traint tegelijk de rust om berekeningen doordacht te benaderen, ook als de druk even oploopt.
Oude ezelsbruggetjes
Veel mensen zijn bekend met het ezelsbruggetje “Meneer Van Dalen Wacht Op Antwoord” voor de rekenvolgorde. Ook “Hoe Moeten Wij Van De Onvoldoendes Afkomen?” wordt vaak gebruikt in de klas en helpt om de juiste volgorde moeiteloos en zonder aarzeling toe te passen.

Ezelsbruggetjes maken abstracte regels concreter en makkelijker te onthouden, niet alleen in wiskunde, maar ook in vakken waar structuur en volgorde belangrijk zijn. Dit toont dat wiskunde draait om helderheid, consistentie en logische stappen.
Ze benadrukken dat wiskunde draait om logisch redeneren in korte, duidelijke stappen die samen één sluitende redenering vormen, wat zowel leerlingen als volwassenen helpt om basisregels beter te begrijpen en met vertrouwen toe te passen wanneer nodig.
Eerst haakjes
De eerste stap in elke berekening is het uitwerken van haakjes, omdat die de prioriteit van bewerkingen aangeven. In deze som komen geen haakjes voor, dus je kunt deze stap overslaan en direct door naar de volgende regel in de volgorde.

Haakjes markeren welk deel eerst moet en voorkomen dat losse stappen door elkaar gaan lopen. Omdat ze hier ontbreken, blijft de berekening overzichtelijk en kan de volgorde zonder extra markeringen worden gevolgd.
Bij complexere berekeningen kunnen haakjes de uitkomst sterk beïnvloeden. Controleer dus altijd als eerste of ze aanwezig zijn en werk ze zorgvuldig uit om tot een betrouwbare en herhaalbare uitkomst te komen.
Machtsverheffen overslaan
Haakjes in formules vergroten de kans op een correcte uitkomst, vooral bij meetkundige berekeningen en langere formules. Ze maken de rekenvolgorde zichtbaar en voorkomen onnauwkeurige stappen.

Na de haakjes volgen normaal gesproken machtsverheffen en worteltrekken, maar aangezien deze som geen machten of wortels bevat, kun je die stap overslaan, wat het geheel compact houdt en de volgende bewerkingen extra duidelijk maakt.
Bij complexere berekeningen, zoals het nauwkeurig bepalen van oppervlaktes of volumes, zijn machten en wortels van groot belang. Het is dan essentieel om de volgorde nauwlettend te volgen en zorgvuldig te rekenen om tot een correct en controleerbaar resultaat te komen.
Vermenigvuldigen
De afwezigheid van deze elementen in de som toont aan dat opgaven waardevol kunnen zijn zonder extra complexiteit. Blijf werken met een gestructureerde aanpak, inclusief een duidelijk stappenplan, overzicht en controleerbare tussenstappen.

Een basisregel is dat vermenigvuldigen en delen vóór optellen en aftrekken komen. Deze afspraak zorgt voor consistente uitkomsten, ongeacht wie de som maakt, zolang iedereen dezelfde volgorde aanhoudt. In dit geval betekent dat eerst 25 × 0 uitrekenen en pas daarna de overige stappen uitvoeren.
Kinderen leren dit principe vroeg en passen het later moeiteloos toe in het voortgezet onderwijs en daarbuiten. Daarom zie je deze regel vaak terug in puzzels en rekenraadsels die logisch denken en wiskundige vaardigheid op een speelse manier willen stimuleren.
De nieuwe som
Nadat de vermenigvuldiging is uitgevoerd, wordt de berekening overzichtelijker en blijven de tussenresultaten duidelijk zichtbaar. Dat maakt het eenvoudiger om het eindantwoord te controleren, eventuele fouten op te sporen en desnoods een stap terug te zetten wanneer iets niet klopt.

50 + 50 – 0 + 2 + 2
“Nu optellen en aftrekken met aandacht en tijd, zodat elke stap klopt en je antwoord goed onderbouwd is. Blijf rustig werken om rekenfouten te voorkomen en de logica zichtbaar te houden.”
Houd vast aan de regel dat optellen en aftrekken van links naar rechts worden uitgevoerd. Zo blijft de berekening eenduidig en kom je, ongeacht wie rekent, consequent op dezelfde juiste uitkomst uit.
Van links naar rechts
Bij optellen en aftrekken werk je stap voor stap en is de leesrichting leidend. Begin je met 50 + 50, dan vormt dat samen 100. Door die vaste volgorde te volgen, houd je de berekening transparant en verklein je de kans op vergissingen wanneer de som langer wordt.

Na het aftrekken van 0 blijft de uitkomst 100. Daarna kun je de resterende stappen op dezelfde manier afwerken en de plusjes rustig optellen om het totaal helder te bepalen zonder twijfel over de volgorde.
Om dit principe echt in de vingers te krijgen, helpt het om regelmatig te oefenen met korte sommen en kleine variaties. Met herhaling ga je de regels automatisch toepassen en groeit het vertrouwen om ze in uiteenlopende situaties correct te gebruiken.
Veel lesprogramma’s besteden extra aandacht aan deze aanpak, zodat kinderen een sterke basis in rekenen opbouwen. Volwassenen passen deze logica later vaak toe in alledaagse berekeningen thuis, op het werk en bij het controleren van bedragen of schema’s.
De laatste stappen
Er resteert nog één onderdeel van de berekening, het slotstuk waarin alle eerdere stappen samenkomen. In deze fase rond je de uitkomst af op basis van de tussentotalen die je zorgvuldig hebt opgebouwd, zodat het antwoord logisch volgt uit wat je al hebt gedaan.

100 + 2 + 2
Het totaal van 104 laat zien hoe belangrijk het is de volgorde van bewerkingen consequent te volgen en geen stappen over te slaan. Een rustige, doordachte aanpak brengt je betrouwbaar bij de juiste uitkomst en maakt uitleg aan anderen eenvoudig.
Veel mensen waarderen juist dit soort korte rekenoefeningen omdat ze snel een kloppend antwoord opleveren en tegelijk een gevoel van succes geven. Dat stimuleert zowel rekenskills als zelfvertrouwen en nodigt uit om vaker te oefenen.
Het juiste antwoord
De correcte uitkomst is 104. Controleer zorgvuldig of je een ander getal hebt, en loop de stappen opnieuw door om te achterhalen waar de fout zit. Nauwkeurig werken en de regels volgen zijn cruciaal voor een betrouwbaar resultaat dat controleerbaar is voor iedereen.

Door wiskundeoefeningen stap voor stap te benaderen groeit je vertrouwen in eigen kunnen en wordt redeneren vanzelf helderder. Je pakt ingewikkelder vraagstukken vervolgens met meer zekerheid, overzicht en precisie aan.
Een juiste oplossing werkt motiverend en maakt de drempel om door te gaan lager. Zo wordt rekenen een prettige bezigheid die inzicht, nauwkeurigheid en voldoening combineert in korte, krachtige leermomenten die je op elk moment van de dag kunt inplannen.
Deel je uitkomst
Raadsels worden leuker wanneer je ze samen bekijkt en antwoorden vergelijkt. Dat levert verrassende gesprekken op, scherpt je eigen denkstappen en laat zien hoe verschillende routes tot hetzelfde correcte antwoord kunnen leiden.

Deze soort uitdagingen is bijzonder geschikt voor platforms zoals Facebook en groepsapps, waar mensen graag hun resultaten delen en elkaars denkwijzen bespreken. Hierdoor ontstaat er een gevoel van verbondenheid en wordt de bereidheid om samen te leren versterkt.
Samen oplossen en delen maakt interactie speels en leerzaam. Rekenraadsels maken wiskunde leuk en toegankelijk voor iedereen, ongeacht leeftijd, achtergrond of ervaring.
✨ Key-points
- Rekenraadsels zorgen voor vermaak en uitdaging, en verbeteren je aandacht, geheugen en concentratie.
- Het strikt volgen van de bewerkingsvolgorde voorkomt fouten en helpt verwarring bij complexere berekeningen te vermijden, ook als de druk hoger is.
- Vermenigvuldigen en delen hebben voorrang op optellen en aftrekken volgens de rekenregels voor betrouwbare resultaten.
- Door elke stap consequent en zorgvuldig uit te voeren en tussentijds te controleren, zal de juiste en volledige uitwerking leiden tot het resultaat 104.
- Door regelmatig te oefenen met dit soort puzzels versterk je rekenvaardigheden, herken je patronen sneller en groeit je zelfvertrouwen in het werken met cijfers.
DEEL NU: RAADSEL: 99% van de mensen faalt erin om deze vraag correct te beantwoorden en denkt ten onrechte dat ze het goede antwoord hebben 🤯🧠
Dit stuk is zorgvuldig ontworpen door KijkPortaal, een dynamisch mediaplatform dat zich specialiseert in het leveren van verhalen die niet alleen inspireren maar ook verrijken, uitgezocht uit alle hoeken van de wereld. Zorg dat je niets mist van onze intrigerende content door KijkPortaal te volgen op Facebook. Laat je meeslepen door een wereld vol verhalen die echt impact hebben. 🌍✨
SPECTRUM Magazine Disclaimer
Dit artikel is bedoeld als informatieve en educatieve inhoud. Het vormt geen financieel, juridisch of medisch advies. Hoewel de inhoud met zorg is samengesteld, kan SPECTRUM Magazine geen aansprakelijkheid aanvaarden voor gevolgen van het gebruik van de informatie. Voor persoonlijke vragen of beslissingen is het raadzaam een bevoegde professional te raadplegen.
Facebook Disclaimer
Deze publicatie is niet bedoeld als financieel advies. Lezers bekijken onze artikelen vanuit oprechte interesse en plezier in het ontdekken van nieuwe inzichten.