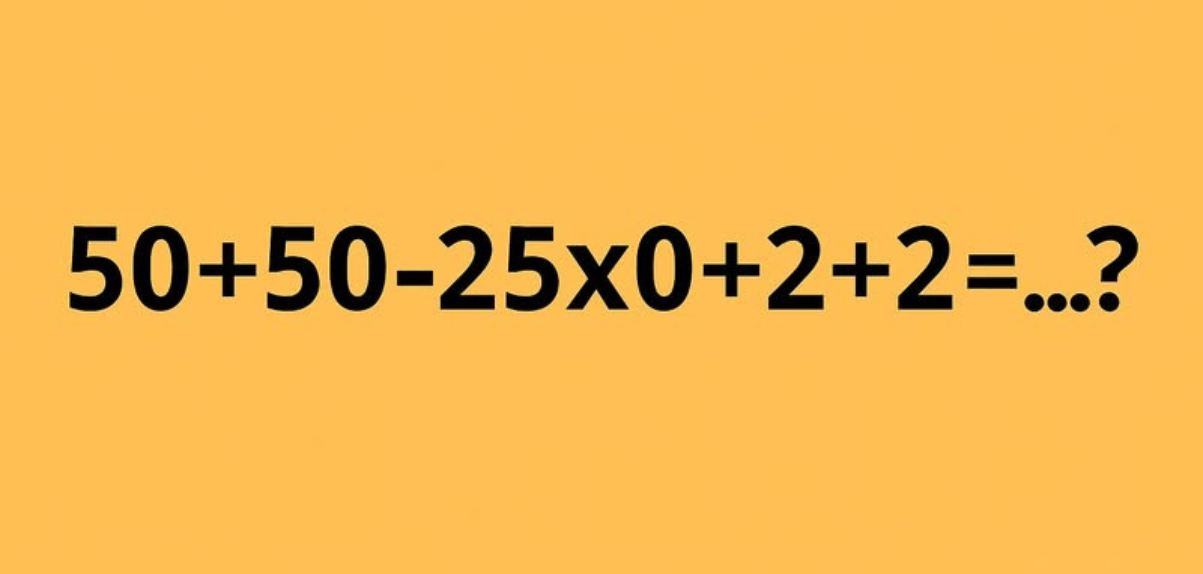Voor velen ligt de schooltijd met rekenschriften al ver achter ons, maar het oplossen van zo’n uitdaging blijft een leuke manier om het brein scherp te houden. Kun jij deze eenvoudige som oplossen en bewijzen dat je nog steeds snel van geest bent, ook zonder jaren wiskunde te hebben gedaan? Laat deze test je denkvermogen prikkelen en toon aan dat tijd en leeftijd geen invloed hebben op een actief en alert brein, maar dat het belangrijk is om je geest te blijven trainen en uit te dagen. Dus ga de uitdaging aan en laat zien dat je mentale scherpte en behendigheid ongeacht je leeftijd behouden is gebleven.
Het oplossen van dit soort puzzels is geliefd bij velen vanwege de speelse en ontspannende manier waarop ze de geest prikkelen. Door je te richten op één doel zonder afleiding, kun je uitdagende situaties aangaan die je mentale scherpte verbeteren. Studies tonen aan dat regelmatig het oplossen van kleine denkopdrachten bijdraagt aan een beter geheugen en een alerter denkvermogen.

Deze rekenvragen zijn speels en geschikt voor alle niveaus, waardoor leren en plezier hand in hand gaan en een positieve ervaring bieden voor iedereen die ze beantwoordt, ongeacht hun achtergrond of vaardigheden op het gebied van wiskunde.

Content:
Waarom raadsels goed zijn
Het oplossen van puzzels is niet alleen een plezierige bezigheid, maar het is tevens uiterst gunstig voor het stimuleren van de hersenen en het vergroten van de concentratie. Wetenschappers benadrukken dan ook het belang van regelmatig puzzelen als essentiële activiteit om scherp te blijven en flexibiliteit in de hersenen te behouden.

Diverse onderzoeken laten zien dat regelmatig puzzelen de cognitieve vaardigheden kan verbeteren. Het stimuleert de herkenning van patronen, helpt bij het vinden van efficiënte oplossingen en zorgt tevens voor ontspanning en plezier, wat een positief effect heeft op het humeur en de algehele gezondheid.
Het oplossen van puzzels versterkt niet alleen de verbinding tussen verschillende delen van de hersenen, maar ook als een effectieve manier om het denkvermogen te trainen. Daarom is het meer dan slechts een spel; het is een positieve gewoonte die de hersenen actief en alert houdt.
De uitdaging
Hoewel de rekensom van vandaag in eerste instantie eenvoudig lijkt, blijkt uit de diverse antwoorden dat de opgave complexer is dan verwacht. De uitdaging bestaat uit het berekenen van de totale oppervlakte van een complexe geometrische figuur, waarbij verschillende variabelen en uitzonderingen moeten worden meegenomen.
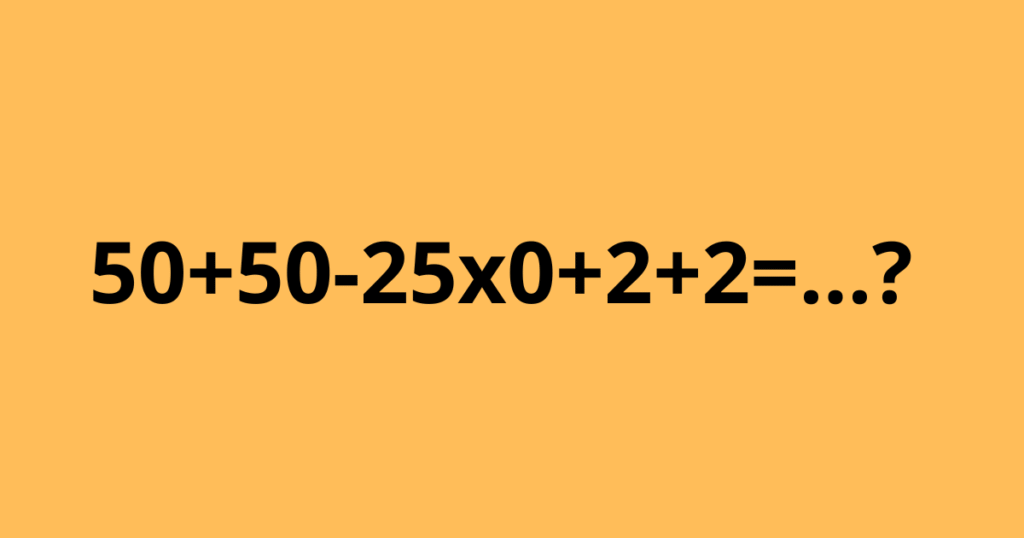
50 + 50 – 25 × 0 + 2 + 2 = ?
Om tot de juiste oplossing te komen, is het essentieel om de juiste volgorde van bewerkingen te volgen. Dit vormt de basis van sterke rekenvaardigheden die op school worden geleerd. Door de stappen nauwkeurig te volgen, kun je een betrouwbare uitkomst verkrijgen.
De opgave laat duidelijk zien dat het belangrijker is om te focussen op logica en structuur dan op snelheid. Door stap voor stap te werken en zorgvuldig te redeneren, zul je sneller en nauwkeuriger resultaten behalen en tegelijkertijd de waarde van kalme en doordachte berekeningen leren waarderen.
Oude ezelsbruggetjes
Veel mensen herinneren zich het ezelsbruggetje “Meneer van Dalen wacht op antwoord” voor rekenbewerkingen. Nu wordt ook “Hoe moeten wij van de onvoldoendes afkomen?” gebruikt. Beide hulpmiddelen zijn effectief voor de juiste volgorde in bewerkingen.

Ezelsbruggetjes maken abstracte regels tastbaar en begrijpelijk, waardoor ze helpen bij het snel begrijpen van berekeningen. Ze worden niet alleen in wiskunde gebruikt, maar ook in andere vakken om informatie beter te onthouden. Zo tonen ze dat wiskunde draait om structuur en helderheid, niet om complexiteit, en helpen ze zowel leerlingen als volwassenen bij het onthouden van basisregels.
Deze boeken laten zien dat wiskunde in essentie draait om het begrijpen van structuur en logisch denken, en niet zozeer om het memoriseren van ingewikkelde formules. Door middel van heldere en beknopte zinnen zijn ze in staat om zowel studenten als volwassenen te helpen bij het begrijpen en toepassen van de basisregels van wiskunde.
Eerst haakjes
Bij een berekening begin je altijd met het oplossen van de haakjes, maar als er geen haakjes zijn, kun je direct doorgaan naar de volgende stap.

De initiële stap in elke berekening is het oplossen van de haakjes, waarbij deze eerste moeten worden berekend vanwege hun prioriteit. Aangezien er geen haakjes aanwezig zijn in dit specifieke voorbeeld, kunnen we deze stap negeren en doorgaan naar de volgende regel.
Haakjes zijn essentieel in ingewikkelde berekeningen. Controleer altijd of er haakjes zijn en werk ze als eerste uit voor een nauwkeurig resultaat.
Machtsverheffen overslaan
Haakjes zorgen voor heldere berekeningen door de volgorde van bewerkingen aan te geven, voorkomen fouten en garanderen nauwkeurigheid. Ze zijn cruciaal bij formules en meetkundige berekeningen voor een juiste uitvoering.

Na de haakjes volgt normaal gesproken het machtsverheffen of worteltrekken, maar in dit geval kunnen we die stap overslaan en direct doorgaan met de berekening, wat het proces vereenvoudigt en overzichtelijker maakt.
Bij uitgebreidere berekeningen, zoals bij het berekenen van oppervlakten of volumes waar machten en wortels juist een belangrijke rol spelen, is het van essentieel belang om nauwgezet de juiste volgorde van bewerkingen te volgen om tot nauwkeurige en correcte resultaten te komen.
Vermenigvuldigen
Het feit dat deze elementen ontbreken in de huidige som toont aan dat niet iedere berekening complex hoeft te zijn en dat zelfs een eenvoudige som inzicht kan verschaffen. Door de gestructureerde aanpak van de berekening blijft het proces helder en overzichtelijk, ongeacht hoe moeilijk de som is die wordt opgelost.

Een van de fundamentele basisprincipes van de wiskunde is dat vermenigvuldigen en delen altijd vóór optellen en aftrekken plaatsvinden, omdat deze volgorde helpt bij het handhaven van betrouwbare en consistente berekeningen, op voorwaarde dat de regel consequent wordt gevolgd.
Zelfs op jonge leeftijd leren kinderen al snel dit principe te begrijpen en toe te passen, aangezien het een cruciaal element is van logisch en gestructureerd rekenen. Hierdoor wordt deze regel vaak gebruikt in puzzels en rekenraadsels die bedoeld zijn om wiskundig inzicht en logisch denken te bevorderen, waardoor kinderen op een speelse en interessante manier getraind worden in het oplossen van rekenkundige vraagstukken.
De nieuwe som
Na het nauwkeurig vermenigvuldigen, is het resultaat zichtbaar en essentieel voor de nauwkeurigheid en controleerbaarheid van de berekening, waardoor fouten worden geminimaliseerd en de betrouwbaarheid wordt gewaarborgd.

50 + 50 – 0 + 2 + 2
Bij het vermenigvuldigen concentreren we ons op optellen en aftrekken. Door zorgvuldigheid in deze stappen te betrachten, kunnen fouten en verlies van overzicht worden voorkomen. Een kalme en geconcentreerde benadering van rekenen leidt tot een betere controle en betrouwbaardere resultaten.
Het is van cruciaal belang om de juiste volgorde bij optellen en aftrekken te hanteren, wat inhoudt dat je altijd van links naar rechts moet werken om verwarring te voorkomen en een consistente uitkomst te garanderen.
Van links naar rechts
Bij het uitvoeren van optellen en aftrekken dien je altijd stap voor stap te werken en van links naar rechts te gaan. Begin met het berekenen van 50 + 50, waarbij je de twee getallen bij elkaar optelt om tot de juiste uitkomst van 100 te komen, en ga vervolgens verder met de rest van de berekeningen op dezelfde systematische manier.

Na het aftrekken van 0 blijft de uitkomst van de berekening 100 over en kun je de volgende stap nemen om de berekening verder te voltooien.
Om dit principe goed te beheersen, is regelmatige oefening en herhaling essentieel. Door dit te doen, zul je merken dat je de regels automatisch gaat toepassen, zonder er bewust over na te hoeven denken.
Veel lesprogramma’s besteden extra aandacht aan het aanleren van de logische aanpak, die kinderen helpt de basisprincipes van rekenen beter te begrijpen en toe te passen. Deze vaardigheden zijn niet alleen nuttig voor kinderen, maar ook voor volwassenen die deze aanpak regelmatig gebruiken in hun dagelijks leven, bijvoorbeeld bij eenvoudige berekeningen thuis of op het werk.
De laatste stappen
Er rest nog één cruciale fase in de berekening, waarbij alle eerdere stappen samenkomen en bijdragen aan de definitieve uitkomst. Hier wordt de uiteindelijke conclusie vastgesteld op basis van verzamelde gegevens en eerder berekende resultaten.

100 + 2 + 2
Dit resulteert in een totaal van 104, wat onderstreept hoe belangrijk het is om de juiste volgorde nauwkeurig te volgen. Het gunstige resultaat van deze berekening bevestigt nogmaals dat een doordachte en gestructureerde aanpak altijd leidt tot een duidelijke en juiste uitkomst.
Veel mensen vinden simpele rekenoefeningen leuk omdat ze gemakkelijk te begrijpen zijn en tegelijkertijd educatief. Het feit dat je direct het juiste antwoord kunt vinden, geeft een gevoel van voldoening en succes, wat helpt bij het versterken van rekenvaardigheden en zelfvertrouwen.
Het juiste antwoord
Het juiste antwoord is 104. Controleer nauwkeurig de stappen als je een ander antwoord krijgt en corrigeer eventuele fouten door de rekenregels precies te volgen.

Met gestructureerd en stap voor stap te werk gaan bij wiskundeoefeningen, behaal je gewenste resultaten en vergroot je zelfvertrouwen, waardoor je complexere vraagstukken met meer zekerheid kunt aanpakken.
Het is inspirerend om de juiste oplossing te ontdekken en enthousiast te blijven oefenen, waardoor rekenen meer wordt dan alleen een praktische vaardigheid.
Deel je uitkomst
Het bespreken en uitwisselen van oplossingen van raadsels met anderen maakt ze leuker en zorgt vaak voor verrassende gesprekken. Probeer antwoorden te vergelijken met vrienden en familie om nieuwe inzichten te krijgen en samen te genieten van een interactieve ervaring.

Op Facebook zijn dit soort uitdagingen erg geliefd, omdat mensen er plezier in hebben om hun antwoorden te delen en nieuwsgierig zijn naar de ideeën van anderen, waardoor een gevoel van verbondenheid ontstaat en samenwerking binnen de online community wordt aangemoedigd.
Door gezamenlijk rekenraadsels op te lossen en ideeën uit te wisselen, ontstaat er een plezierige en leerzame sociale ervaring die wiskunde toegankelijk en aantrekkelijk maakt voor mensen van alle leeftijden en ervaringsniveaus.
✨ Key-points
- Rekenraadsels bieden niet alleen plezier en uitdaging, maar stimuleren ook de hersenen en verbeteren het concentratievermogen.
- Het nauwkeurig volgen van de juiste rekenvolgorde is essentieel om fouten te voorkomen en verwarring bij complexere berekeningen te vermijden.
- Bij het oplossen van een som geldt dat vermenigvuldigen altijd vóór optellen en aftrekken moet plaatsvinden, zoals de standaard rekenregels voorschrijven.
- Wanneer dit correct wordt toegepast, levert de berekening altijd het resultaat 104 op, ongeacht wie de som maakt of welke methode wordt gebruikt.
- Regelmatig oefenen met dit soort puzzels versterkt niet alleen het geheugen, maar ontwikkelt ook rekenvaardigheden en vergroot het zelfvertrouwen in het omgaan met cijfers.
DEEL NU: BEKIJK | Kijkers van Miljoenenjacht zijn geschokt en verontwaardigd door de gebeurtenissen, en vinden ze te schokkend om te beschrijven.
Dit kleinood is met finesse in elkaar getimmerd door Allerlei Plaatjes, het mediaplatform dat de kletspraat overstijgt met echte inhoud. Wij serveren verhalen die niet alleen je blik verruimen, maar ook je denkwereld oprekken, vanuit de meest gevarieerde hoekjes van onze kleurrijke aarde. Klamp je vast voor onze schitterende updates door Allerlei Plaatjes te volgen op Facebook
SPECTRUM Magazine Disclaimer
Dit artikel is bedoeld als informatieve en educatieve inhoud. Het vormt geen financieel, juridisch of medisch advies. Hoewel de inhoud met zorg is samengesteld, kan SPECTRUM Magazine geen aansprakelijkheid aanvaarden voor gevolgen van het gebruik van de informatie. Voor persoonlijke vragen of beslissingen is het raadzaam een bevoegde professional te raadplegen.
Facebook Disclaimer
Deze publicatie is niet bedoeld als financieel advies. Lezers bekijken onze artikelen vanuit oprechte interesse en plezier in het ontdekken van nieuwe inzichten.